
The outer surface defines a region within which frame-dragging is so powerful that even light can only orbit in one direction. Robert Wald of the University of Chicago says that the meaning of these surfaces was “not clear from the Kerr metric written in Kerr’s coordinates.”Ī few years later, analyses showed that only the inner surface is a true event horizon, and that the smaller ring singularity is not accessible to the world outside. In addition, the Kerr metric possesses two surfaces that looked like event horizons, with one nested inside the other but touching at the poles. Whereas the Schwarzschild metric has a central point singularity, the Kerr metric has a singularity that looks like “a ring in the equatorial plane … spinning at the speed of light,” explains Werner Israel of the University of Victoria, Canada. But interpreting the physical significance of some mathematical oddities close to the origin proved difficult. The Kerr metric was clearly a description of spacetime curvature around a spinning mass. By examining the form of the new solution at large distances from the origin and by comparing it to known, approximate solutions for a rotating object, Kerr showed that the second parameter represented angular momentum-essentially, the amount of spin. One corresponded to the mass parameter in the Schwarzschild metric, but the significance of the other was not obvious.
#THE CURVED SPACE FREE#
Exploring a certain class of metrics, he found an exact solution with two free parameters. Roy Kerr, a New Zealand relativist at the University of Texas in Austin and Wright-Patterson Air Force Base in Ohio, came at the problem from a different angle. A complete solution to the Einstein equations for a rotating body would have the symmetry of a cylinder, but even this modest departure from spherical symmetry made solving the equations fearsomely difficult.
An example is that bodies traveling around the Earth on identical orbits, but in opposite directions, will measure slightly different times for one circuit. In 1918 theorists used approximate methods to show that a rotating mass also distorts spacetime via an effect called frame dragging.

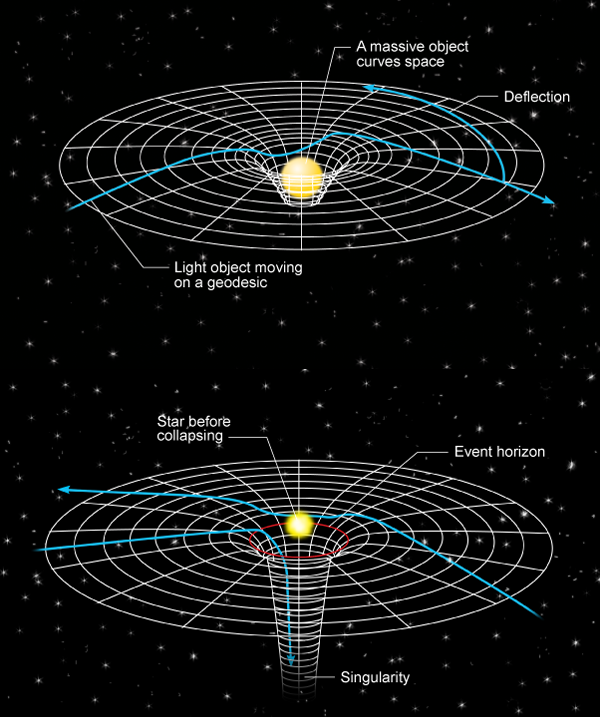
This metric is now known as the description of a static black hole (see 2004 Focus Landmark). Mathematicians eventually showed that Schwarzschild’s metric had a central singularity-corresponding to a finite mass packed into a point-and a surrounding spherical surface called the “event horizon” at what became known as the Schwarzschild radius. That same year, the German mathematical physicist Karl Schwarzschild found a spherically symmetric solution for empty space, with no time variation but with curvature everywhere. On the surface of a sphere, for example, the Pythagorean answer is always too small.Įinstein published his theory of gravitation in 1916.
#THE CURVED SPACE HOW TO#
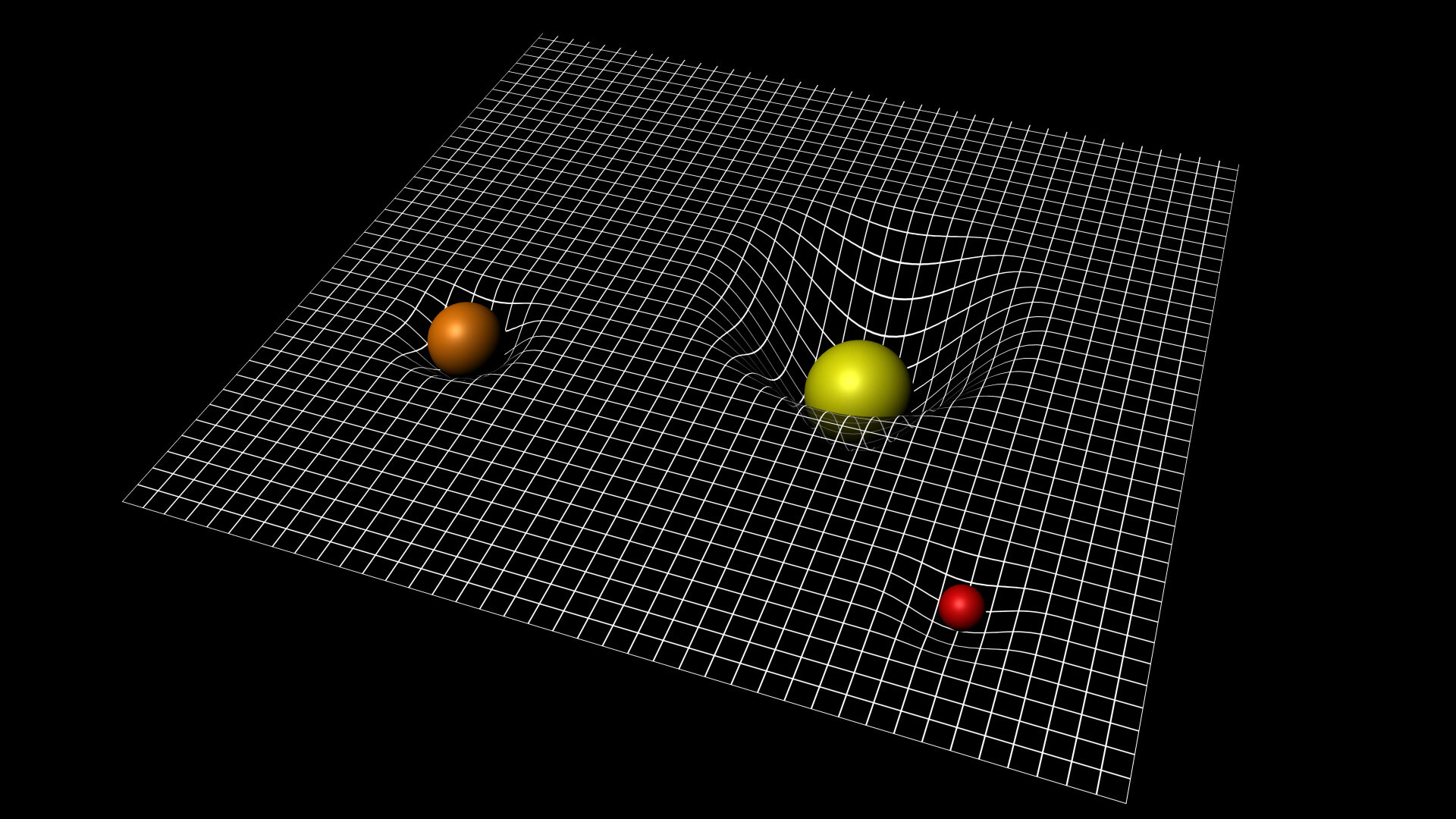
Solutions to Einstein’s general relativity equations describe the curvature of space with a mathematical function called the metric tensor, or “metric.” Given the coordinates of two points in space, the metric tells you how to compute the distance between them, since the usual Pythagorean theorem doesn’t apply in curved space. Since all black holes spin, this solution has been essential to astrophysicists studying the behavior of black holes and of matter in their vicinity. Analysis over the following years showed it to be the unique description of curved spacetime around a spinning black hole. One important solution appeared in Physical Review Letters in 1963. The math is intricate, so exact solutions to Einstein’s equations are rare. General relativity describes how mass and energy induce curvature in spacetime. Landmarks articles feature important papers from the archives of the Physical Review journals. A jet of debris flies outward from the center. This drawing shows the disk of debris falling into a spinning, supermassive black hole at the center of a galaxy. In 1963 Roy Kerr provided the mathematical function that describes the curvature of spacetime around a spinning black hole-a major step for both general relativity and for astrophysics.


 0 kommentar(er)
0 kommentar(er)
